Интерпретатор частично рекурсивных функций (Дмитрий Астраханцев, OSEDUCONF-2024)
Материал из 0x1.tv
- Докладчик
- Дмитрий Астраханцев
В работе предлагается язык, основанный на концепции использования частично рекурсивных функций, описан его синтаксис и реализация его интерпретатора.
Данный язык предлагается использовать для включения в курсы по программированию и расширения понятия Тьюринг полноты, знакомства с основами функционального подхода к программированию.
Содержание
Видео
Презентация
Thesis
Введем базовые понятия и определения[1][2].
Классом частично рекурсивных функций называется класс функций, которые могут быть получены путём применения трёх операций (суперпозиции, примитивной рекурсии и минимизации) к трём базовым функциям (функции тождественного нуля, функции следования и функции выбора).
Базовыми рекурсивными функциями называются функции:
- Тождественный ноль:
- Функция следования:
- Функции выбора: ()
Операции над функциями называются:
- Суперпозиция
- ():
- Примитивная рекурсия
- ():
- Минимизация
- ():
Основным достоинством класса частично рекурсивных функций является тот факт, что он совпадает с классом
вычислимых по Тьюрингу функций. Другими словами, множество всех частично рекурсивных функций совпадает
со множеством всех функций, которые могут быть реализованы машиной Тьюринга[3].
Таким образом, изучение частично рекурсивных функций может быть использовано для демонстрации студентам первых курсов высших учебных заведений основных принципов функционального программирования без необходимости изучать для этого какой-либо функциональный язык. Однако для этого необходимо наличие программного обеспечения, которое могло бы вычислять функции, записанные с помощью базовых функций и операций над ними.
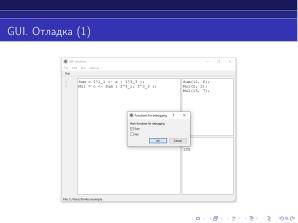
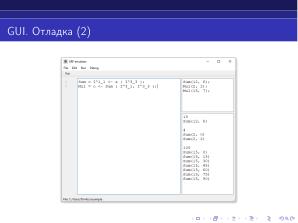
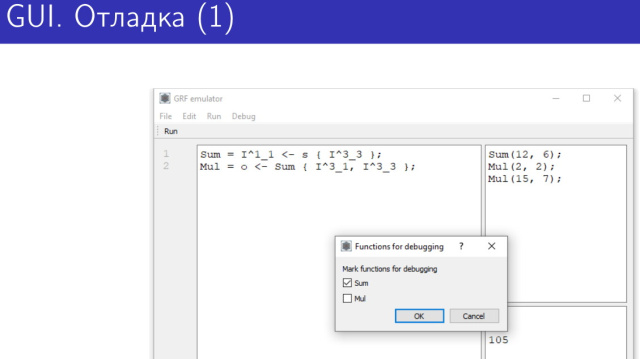
Целью данной работы ставилось предоставление такого программного обеспечения. Очевидно, что оно должно включать в себя язык, который был бы основан на частично рекурсивных функциях и только на них, его интерпретатор, графический интерфейс и средство отладки.
В ходе данной работы был разработан именно такой язык и средства работы с ним. Язык включает в себя
- Базовые функции
- Функция тождественного нуля, обозначаемая o.
- Функция следования, обозначаемая s.
- Функция выбора, обозначаемая I\^{<n>_{}.
- Операции
- Операция суперпозиции, обозначаемая F\{G, H, K\}.
- Операция примитивной рекурсии, обозначаемая F <- G.
- Операция минимизации, обозначаемая ?F.
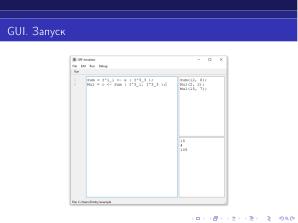
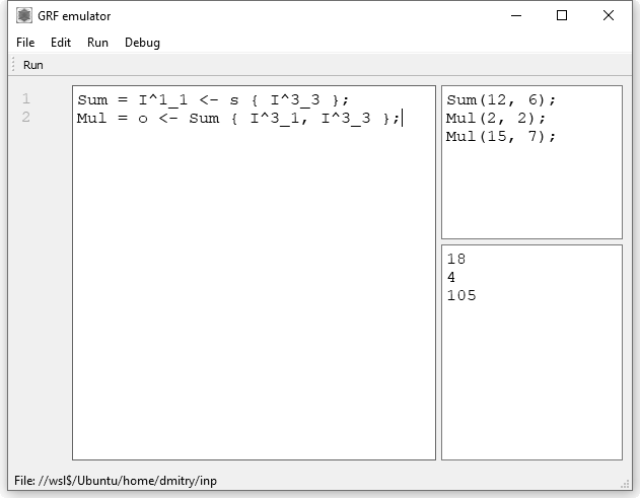
Графический интерфейс:
Получившийся язык носит декларативный характер, и эту особенность было решено подчеркнуть, полностью отделив вызов функций от их определения. Для этого вызов функций был перенесён в отдельное окно графического интерфейса.
Таким образом, графический интерфейс приобретает деление на 3 области: определения функций, вызова функций и вывода результатов, ошибок и отладочной информации.
Примечания и ссылки
- ↑ Мальцев А. И. Алгоритмы и рекурсивные функции. 2-е изд. М. : Наука. Гл. ред. физ.-мат. лит., 1986. 368 с.
- ↑ Петер Р. Рекурсивные функции // Под ред. и с пред. Колмогорова А. Н. М. : Издательство иностранной литературы, 1954. 264 с.
- ↑ Верещагин Н. К., Шень А. Лекции по математической логике и теории алгоритмов. Часть 3. Вычислимые функции. 4-е изд., исправленное. М. : МЦНМО, 2012. 160 c.